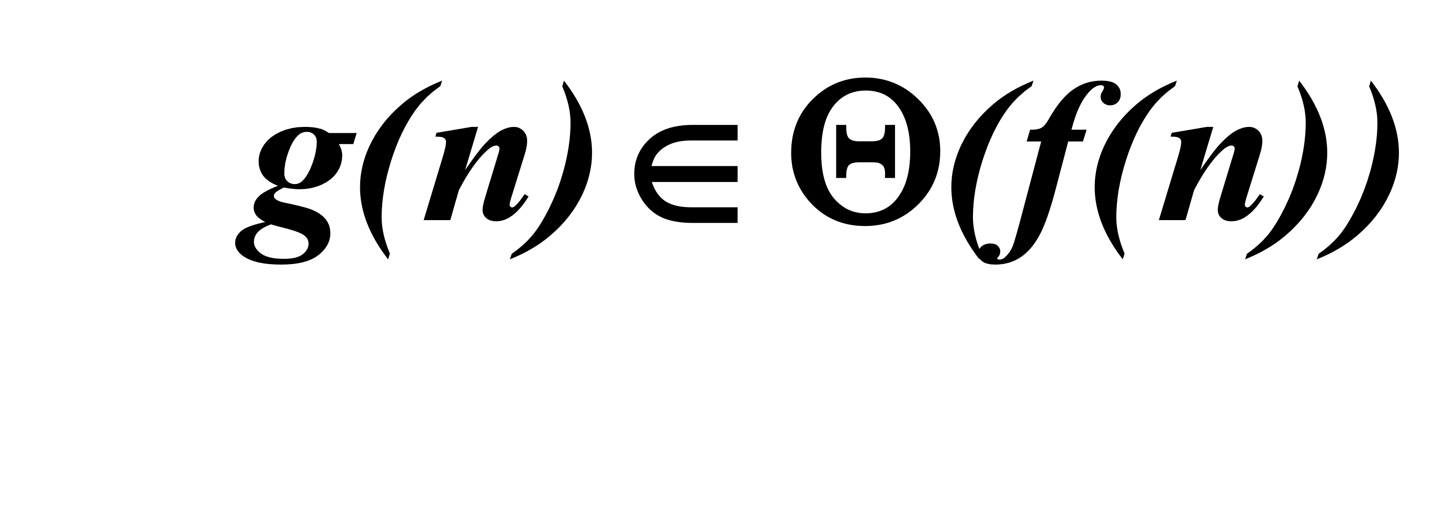백투더코딩

소수: 1과 자기자신(n)만을 약수로 가지는 수

방법 1) 2~n-1까지 모든 수를 다 나눠보며 나눠 떨어지지 않으면 소수다.

방법 2) 메모제이션 이전까지의 모든 소수로 나눠 떨어지지 않으면 그 수는 소수다.

방법 3) 제곱근 2~루트n 사이의 수를 다 나눠보며 나눠 떨어지지 않으면 소수다.

방법 4) 에라토스테네스의 체  n^1/2 이하의 수의 배수를 다 지운후 남아있는 수가 소수다.

참고사이트

https://velog.io/@hyeon930/%EC%86%8C%EC%88%98%EB%A5%BC-%EA%B5%AC%ED%95%98%EB%8A%94-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

https://coding-factory.tistory.com/367

https://danidani-de.tistory.com/50

구글링을 하다가 우연히 endl을 통해 개행을 할 경우 출력과 함께 버퍼를 지워 속도가 

더 느리다는 게시글을 봤다.

endl 대신 C언어에서 사용했듯이 '\n'을 통해 개행을 진행하면 실행 속도를 향상 시킬 수 있다.

참고사이트 

https://jaimemin.tistory.com/1521

최대공약수: 공통된 약수 중 가장 큰 수

유클리드 호제법 이용

R이 0이 될 때까지

A % B = R

A = B

B = R 

반복하고 마지막 A가 최대 공약수가 된다.

최소공배수: 공배수 중에서 가장 작은 수

A*B/최대공약수 이용  (최소공배수 * 최대공약수 = A * B이기 때문에)

=>A*B/gcd(A, B)

참고 사이트

https://twpower.github.io/69-how-to-get-gcd-and-lcm

mod 연산을 사용하여 나머지 연산을 구한다.

a mod b : a를 b로 나눈 나머지

• (A + B) % M = ((A%M) + (B%M)) % M
• (A X B) % M = ((A%M) X (B%M)) % M
• (A - B) % M = ((A % M) - (B % M) + M) % M

뺄셈 연산의 경우만 mod 연산을 수행한 값이 음수가 나올 수 있으므로 굵은 글씨 부분을 추가해야 한다.

ex) -5 mod 3 은 값이 1이 나와야 한다. (-2+3=1)

참고사이트

https://velog.io/@gidskql6671/%EB%82%98%EB%A8%B8%EC%A7%80Modulo-%EC%97%B0%EC%82%B0-%EB%B6%84%EB%B0%B0%EB%B2%95%EC%B9%99

https://codingram.tistory.com/26

https://teus.me/736

빅오 표기법 사용

ex) O(N)

Big O

g(n)<=c*f(n):asymptotic upper bound

(c:some positive real constant N:some nonnegative integer s.t. for all n>=N)

g(n) is big O of f(n)

시간 복잡도를 계산할 때 상수는 버리며 가장 차수가 큰 변수를 기준으로 한다.

ex) n^2 와 n이 있을 경우 n^2이 빅오 표기법에 사용됨.

시간복잡도와 달리 공간 복잡도는 알고리즘 문제에서 크게 상관이 없는 경우가 많지만

필요없는 공간을 사용하고 있진않은지 신경을 쓸 필요는 있다.

Big O 시간의 상한(최악)

g(n)<=c*f(n):asymptotic upper bound

(c:some positive real constant N:some nonnegative integer s.t. for all n>=N)

g(n) is big O of f(n)

Omega 시간의 하한(최선)

g(n)>=c*f(n):asymptotic lower bound

(c:some positive real constant N:some nonnegative integer s.t. for all n>=N)

g(n) is omega of f(n)

Order 시간의 평균

c*f(n)<=g(n)<=d*f(n)

(c,d:some positive real constant N:some nonnegative integer s.t. for all n>=N)

g(n) is order of f(n)

오더를 빅오로 사용하는 경우가 많습니다.

참고 사이트

https://memostack.tistory.com/57